完整CLion下工程，见GitHub

问题描述

马踏棋盘问题即在一个8*8的棋盘上，指定一个起点，找到一个路径，让棋子按照马走日的规则将所有格子无重复的遍历一次。
这个问题是在学习数据结构与算法的时候看到的，当时看的是C语言的版本，也没记住具体的解法，事后回顾起来觉得很有意思，于是自己用C++编写了一段代码尝试一下。

分析

• 首先进行分析：从数据结构的角度来分析，一个棋盘可以看作一个二维数组。然后是对每次落子进行分析，根据马走日的规则，假设不考虑是否会出现越界情况，则在某位置X上，下一步落子共有八种可能性，如图所示，按照顺时针顺序依次标记为0，1，2，3，4，5，6，7：
  
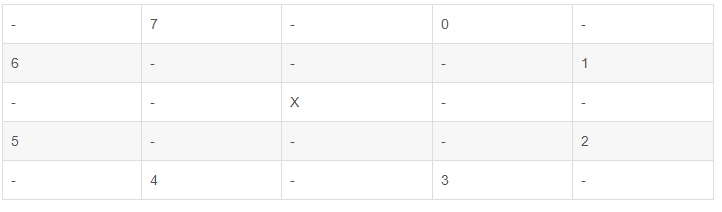
  那么显然易见，已知X的情况下，利用深度优先遍历的方式，是一定可以得到一个路径满足要求的，只不过这么做的计算复杂度非常之高。有了想法，当然是以能跑出结果为导向先写出大概的代码才行，于是我按照这个思路写出了原始版本：

实现与优化

/*
 * 马踏棋盘最原始的深度优先算法
 * 利用栈
 */
#include <iostream>
#include <chrono>
#include <stack>
#include <assert.h>
#include <cstring>
using namespace std;
const int chessX = 8;
const int chessY = 8;
static bool chess[chessX][chessY];//棋盘，遍历过的位置进行标记
struct Id{
    int x;
    int y;
    Id(int theX,int theY):x(theX),y(theY) {};
    ~Id() = default;
};
stack<Id> step;//栈，依次存放每次遍历的坐标，回溯的时候出栈
bool run(int,int);
int judge(int,int,int &);//判断路径，返回0-7表示选择的路径，返回则需要回溯
bool isInChess(int,int,int);//判断某个方向的落子是否在棋盘内
bool isNeverRun(int,int,int);//判断落子是否被遍历过
Id next(int,int,int);//返回cnt方向的落子位置
int main()
{
    memset(chess,0x00,sizeof(chess));
    auto start = chrono::system_clock::now();
    run(0,7);
    auto end = chrono::system_clock::now();
    auto duration = chrono::duration_cast<chrono::microseconds>(end-start);
    /*
    for(int i=0;i<chessX;++i)
    {
        for(int j = 0;j<chessY;++j)
            cout << chess[i][j];
        cout << endl;
    }*/
    if(step.size()==0)
    {
        cout << "can not complete!" << endl;
        return 0;
    }
    int res[chessX][chessY] = {0};
    for(int i=0;i<chessX*chessY;++i)
    {
        res[step.top().x][step.top().y] = chessX*chessY-i;
        step.pop();
    }
    for(int i=0;i<chessX;++i)
    {
        for(int j = 0;j<chessY;++j)
            cout << res[i][j] << '\t';
        cout << endl;
    }

    cout << double(duration.count())* chrono::microseconds::period::num/
         chrono::microseconds::period::den
         << "秒" << endl;
    return 0;
}

bool run(int x,int y)
{
    int cnt = 0;
    bool finish;
    step.push(Id(x,y));
    chess[x][y] = true;
    if(step.size()>=chessX*chessY)
        return true;
    while(judge(x,y,cnt)<8)
    {
        Id nextId = next(x,y,cnt);
        finish = run(nextId.x,nextId.y);
        if(finish)
            return true;
        else
            ++cnt;
    }
    //finish==false
    step.pop();
    chess[x][y] = false;
    return false;
}

int judge(int x,int y,int &cnt)
{
    while(cnt<8)
    {
        if(isInChess(x,y,cnt)&&isNeverRun(x,y,cnt))
            return cnt;
        else
            ++cnt;
    }
    return cnt;
}

bool isInChess(int x,int y,int cnt)
{
    assert(cnt<8&&x>=0&&x<chessX&&y>=0&&y<chessY);
    switch(cnt)
    {
        case 0:
            return (x+1<chessX)&&(y+2<chessY);
        case 1:
            return (x+2<chessX)&&(y+1<chessY);
        case 2:
            return (x+2<chessX)&&(y-1>=0);
        case 3:
            return (x+1<chessX)&&(y-2>=0);
        case 4:
            return (x-1>=0)&&(y-2>=0);
        case 5:
            return (x-2>=0)&&(y-1>=0);
        case 6:
            return (x-2>=0)&&(y+1<chessY);
        case 7:
            return (x-1>=0)&&(y+2<chessY);
        default:
            cerr << "error:isInChess" << endl;
            return 0;
    }
}

bool isNeverRun(int x, int y, int cnt)
{
    switch (cnt)
    {
        case 0:
            return !chess[x+1][y+2];
        case 1:
            return !chess[x+2][y+1];
        case 2:
            return !chess[x+2][y-1];
        case 3:
            return !chess[x+1][y-2];
        case 4:
            return !chess[x-1][y-2];
        case 5:
            return !chess[x-2][y-1];
        case 6:
            return !chess[x-2][y+1];
        case 7:
            return !chess[x-1][y+2];
        default:
            return false;
    }
}

Id next(int x, int y, int cnt)
{
    switch (cnt)
    {
        case 0:
            return Id(x+1,y+2);
        case 1:
            return Id(x+2,y+1);
        case 2:
            return Id(x+2,y-1);
        case 3:
            return Id(x+1,y-2);
        case 4:
            return Id(x-1,y-2);
        case 5:
            return Id(x-2,y-1);
        case 6:
            return Id(x-2,y+1);
        case 7:
            return Id(x-1,y+2);
        default:
            cerr << "next func error";
            return Id(x,y);
    }
}

• 这么一个代码的框架就算是搭起来了，那么运行结果呢，在运算8*8的棋盘时，部分点算不出来，就是 那种算几个小时都出不来的情况，有的点可以在几秒内算出来，如下：
  
• 当然这种效率是很捉急的，于是查阅了相关的优化方式，发现可以使用贪婪算法对其进行优化，加快其运行速度，另一方面，这个原始版本还有其他不足，本就想做些小修改，于是我就立刻写下了另一个优化版本。
• 先简单介绍下贪婪算法，贪婪算法就是每一步都选取局部的最优解，从而最终使得最终解逼近完美解。在本问题下，贪婪算法的执行效果就是，检测下一步可能落子的下一步可落子位置数，数量越少的，优先级越高。比如现在棋子在A点，A点下一步可以落在BCD三个点上，并且B的下一步可能有2个位置，C和D可能有3个位置，那么B的优先级就比C和D要高，我们优先选择B。
  代码修改如下：

/**
 * 马踏棋盘优化：
 * 1.DFS，对原有的结构进行改进
 * 2.选择下一步的方式采取贪婪算法，即考察每一个备选落子下一步的可落子位置数，
 * 位置数少的优先落子。
 */
#include <iostream>
#include <chrono>
#include <map>
#include <assert.h>
#include <vector>

using namespace std;

const int chessX = 8;
const int chessY = 8;
int chess[chessX][chessY] = {0};
int cnt = 0;//表示深度，表示走的步数
int fx[8] = {1,2,2,1,-1,-2,-2,-1};
int fy[8] = {2,1,-1,-2,-2,-1,1,2};
typedef int Direct;//定义新的数据类型，方便表示，0-8表示8个落子方向
typedef multimap<int,Direct> nextMap;//存放每个位置下一个落子优先级的数据
typedef nextMap::iterator nIter;//定义迭代器类型
bool run(int,int);//递归主函数
nextMap judge(int,int,int&,int&);//返回下一个落子位置的优先级,并且在keyvmin里存放key值的非0最小值
bool isOk(int,int,Direct);//判断坐标是否可用：1.没遍历过2.没有超出棋盘
int main()
{
    int x,y;
    vector<int> iveco;

    cout << "请输入初始坐标x：" << "(x>=0&&x<" << chessX << ")" << endl;
    cin >> x;
    assert(x>=0&&x<chessX);
    cout << "请输入初始坐标y: " << "(y>=0&&y<" << chessY << ")" <<endl;
    cin >> y;
    assert(y>=0&&y<chessY);
    auto start = chrono::system_clock::now();
    run(x,y);
    auto end = chrono::system_clock::now();
    auto duration = chrono::
    duration_cast<chrono::microseconds>(end-start);
    for(int i = 0;i<chessX;++i)
    {
        for(int j=0;j<chessY;++j)
            cout << chess[i][j] << '\t';
        cout << endl;
    }
    cout << double(duration.count())* chrono::microseconds::period::num
            /chrono::microseconds::period::den
         << "秒" <<endl;
    return 0;
}

bool run(int x, int y)
{
    int keyMin = 8;
    int keyMax = 0;
    bool finish;
    chess[x][y] = ++cnt;
    if(cnt>=chessX*chessY)
        return true;
    nextMap next = judge(x,y,keyMin,keyMax);
    for (int i = keyMin; i <= keyMax ; ++i)
    {
        if(next.count(i)!=0)
        {
            nIter beg = next.lower_bound(i);
            nIter end = next.upper_bound(i);
            for(nIter j = beg;j!=end;++j)
            {
                finish = run(x+fx[j->second],y+fy[j->second]);
                if(finish)
                    return true;
            }
        }
    }
    chess[x][y] = 0;
    --cnt;
    return false;
}

nextMap judge(int x, int y,int &keyMin,int &keyMax)
{
    nextMap res;
    keyMin = 8;
    keyMax = 0;
    for(int i=0;i<8;++i)
    {
        if(isOk(x,y,i))
        {
            int xx = x + fx[i];
            int yy = y + fy[i];
            int cnt = 0;
            for(int j=0;j<8;++j)
            {
                if(isOk(xx,yy,j))
                    ++cnt;
            }
            res.insert(make_pair(cnt,i));
            if(keyMin>cnt)
                keyMin = cnt;
            if(keyMax<cnt)
                keyMax = cnt;
        }
    }
    return res;
}

bool isOk(int x1, int y1,Direct direct)
{
    int x = x1+fx[direct];
    int y = y1+fy[direct];
    return chess[x][y] == 0 && x >= 0 && x < chessX && y >= 0 && y < chessY;
}